Dimenzování serv u modelů letadel
Tento příspěvek vznikl jako reakce na nekonečné diskuze mezi modeláři na téma jak silná serva jsou potřebná především pro obří modely letadel a makety.
Několik poznámek pro pochopení problematiky:
Již ze základní školy si pamatujeme z hodin fyziky princip páky, který vtipně používali již naši pravěcí předkové. Skutečnost, že stejné práce dosáhneme působením menší síly na delší dráze pomocí pákového převodu a naopak je nám dostatečně známa, stejně jako definice točivý moment = síla x páka.
Točivý moment serva je tedy: Mt = (páka serva / páka kormidla ) x točivý moment kormidla.
Poznámka: Výrobci serv udávají točivý moment serva ve vžitých jednotkách – kilogramcentimetrech. Správnější by pro vyjádření momentu bylo použít jednotku síly Newton, nikoli jednotku hmotnosti kilogram, pro přepočet momentu poslouží přibližný vztah 1 kg.cm = 10 N.cm. Můžete se také setkat s anglosaskými jednotkami – 1 oz.in ( unce x palec ) = 28,3g x 2,54cm = 72g .cm = 0,72 N.cm, 100 oz.in = 7,2 kg . cm
Příklad: Točivý moment serva HS 422 Mt=4,1 kg/cm (tedy servo při délce páky 1 cm vyvine sílu 4,1 kg resp. správněji 41 N, při délce páky 3 cm to ale bude jen třetina: F=4,1/3=1,4 kg). Servo má využitelnou výchylku 60°, na ovládané ploše potřebujeme výchylku 30°, můžeme tedy využít pákový převod v poměru 1:2 k dosažení dvojnásobného točivého momentu na ovládané ploše při daném točivém momentu serva.
Výpočet momentu serva:
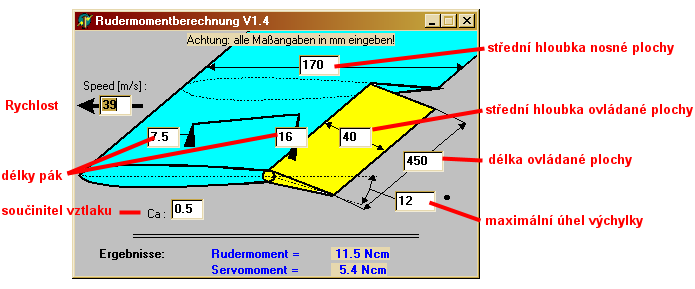
Na webu Dietricha Meissnera najdete jednoduchou freewarovou utilitku Rudermomentberechnung V1.4 , která dává jednoduchou a názornou odpověď. Ovládání je velmi jednoduché, stačí dosadit známé hodnoty geometrických rozměrů letadla v milimetrech, délky pák serva a ovládané plochy jsou samozřejmě myšleny od osy otáčení po osu čepu táhla. Jediná neznámá veličina v tomto výpočtu je součinitel vztlaku Ca, který závisí na profilu a úhlu náběhu nosné plochy, je tedy zřejmé, že za letu se jeho hodnota může značně měnit podle aktuálního letového režimu. Neuděláme velkou chybu, když zvolíme obvyklou hodnotu cca 0,5 ale musíme si být vědomi, že v hraničních podmínkách může u běžných profilů dosáhnout hodnoty až 2. Ostatně v programu si můžete snadno ověřit, v jakých hodnotách se pohybuje výsledný točivý moment serva v závislosti na změně Ca. Například servo klapky při přistání s velkým úhlem náběhu může být namáháno skutečně úctyhodnými silami, i když tomu mnozí modeláři nechtějí věřit.
Pro ilustraci dále uvedu porovnání výsledků výpočtu s doporučením výrobce modelu VELOX II 2,2m od firmy Orion models. Zde jsou rozměry modelu (PDF). Součinitel vztlaku Ca volím 0,5. Rychlost letu lze odhadnout na základě stoupání vrtule a otáček motoru za letu, uvažujeme vždy nejrychlejší možnou variantu (let „s kopce“, odlehčení motoru – otáčky n = cca 7500/min, stoupání vrtule s = 10″ = 0,254m, V=n.s/60= 32 m/s).
- Křidélko: Délka 990mm, páka serva: 28mm, páka křidélka: 28mm, stř. hloubka křídla: 424mm, stř. hloubka křidélka: 90mm, max. výchylka 20°. Výsledek: M=132N.cm=13,2kg.cm
- Výškovka: Délka 350mm, páka serva: 28mm, páka kormidla: 28mm, stř. hloubka VOP: 285mm, stř. hloubka kormidla: 120mm, max. výchylka 20°. Výsledek: M=68N.cm=6,8kg.cm
- Směrovka: Délka 400mm, páka serva: 35mm, páka kormidla: 35mm, stř. hloubka SOP: 400mm, stř. hloubka kormidla: 180mm, max. výchylka 30°. Výsledek: M=180N.cm=18kg.cm
ZÁVĚR :
- Točivé momenty potřebné pro ovládání modelu Velox II 2,2m stanovená výpočtem jsou prakticky tožné s doporučením výrobce modelu( OM ): křidélka 11kg.cm, VOP 6kg.cm, SOP 16kg.cm. Je zřejmé, že nejsou doporučovány žádné zbytečně vysoké hodnoty, jak je často modeláři zlehčováno!
- Nepoužívejte slabší serva pokud chcete, aby servo vydrželo dlouho spolehlivě fungovat. Poddimenzovaná serva budou mít sníženou životnost!
- Na svém modelu VELOX II 2,2 m mám použita serva: Křidélka: HS-645 MG (9,6kg.cm)-2x, VOP: HS-475 HB (6kg.cm)-2x, SOP: HS-805 BB (25kg.cm)
- Z důvodu omezení vlivu vůlí volím páky co největší. Síla v táhle s ramenem páky klesá, ale točivý moment se tím nemění.
- Křidélkové servo začalo mít velké vůle v převodech a musel jsem je vyměnit, důvod je s nejvyšší pravděpodobností ten, že jsem použil slabší servo než vychází z výpočtu.
- Rychlost serv není stálá a obecně platí, že při 2/3 zatížení vzhledem k maximálnímu točivému momentu je rychlost zhruba poloviční a při maximálním momentu se rychlost zmenší cca 5x, viz tento článek (tyto skutečnosti byly uvedeny v RC Revue 2/2002), takže prakticky je využitelný točivý moment, který dosahuje asi 2/3 maximálního udávaného momentu serva.